k空間のデータ充填方法についてです。
問題
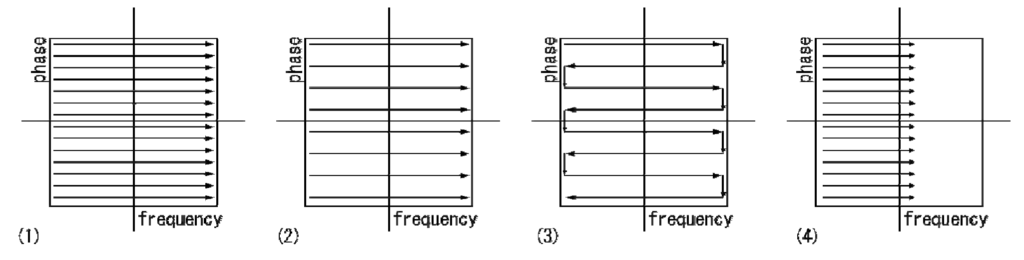
次のk空間のデータ充填方法を示した図において、正しい記述を選択してください。
a.(1)は(2)よりも位相方向のFOVが大きい。
b.(1)は(4)よりも周波数方向のFOVが大きい。
c.(3)は(2)よりも撮像時間が短い。
d.(4)は(1)よりも撮像時間が短い。
e.(2)は(1)よりもSNRが高い。
解答
a,c
解説
k空間はなぜ必要か
レントゲンでは被写体にX線を照射し、透過したX線から直接画像を作成します。しかしMRIはRFパルスを照射しても直接画像化することは出来ないのです。
被写体を静磁場環境におきRFパルスで1H原子核を共鳴させます。次に位置情報を得るために傾斜磁場を印加させるのですが、ここで信号はフーリエ変換されk空間に入ることになります。その後逆フーリエ変換を行いMR画像が作成されます。
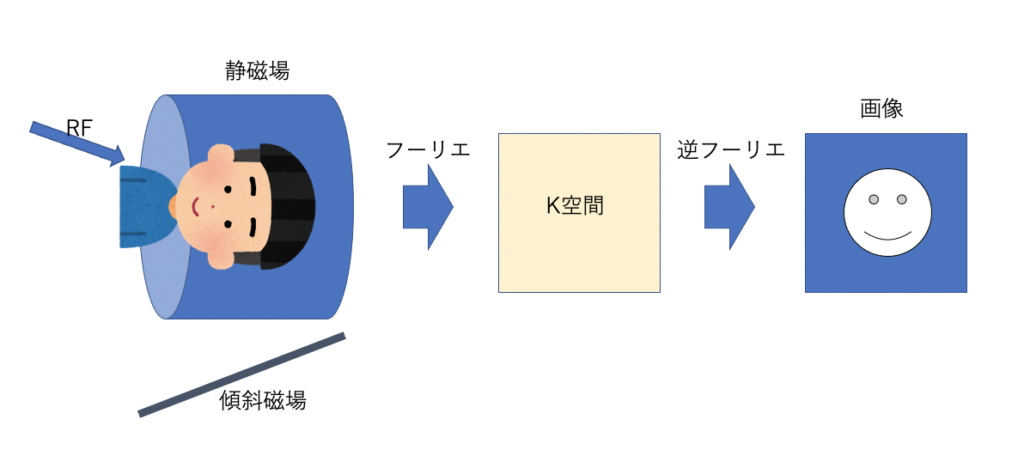
そのためMR画像を作る過程でk空間は必要不可欠となっています。
k空間の特徴
k空間はエルミート対象といって上下左右の信号が関係し合っています。単純な線対象、点対象ではありませんが、偶関数の余弦波と奇関数の正弦波によりこの様な関係となっています。
そのため理論的には、第一象限(どこかの1/4)のデータさえあれば画像ができることとなります。しかし、実際にはそう甘くなく、磁場の不均一性や体動などが影響し性格なエルミート対象とはなっていません。結局半分とちょっとのデータが必要となってきます。
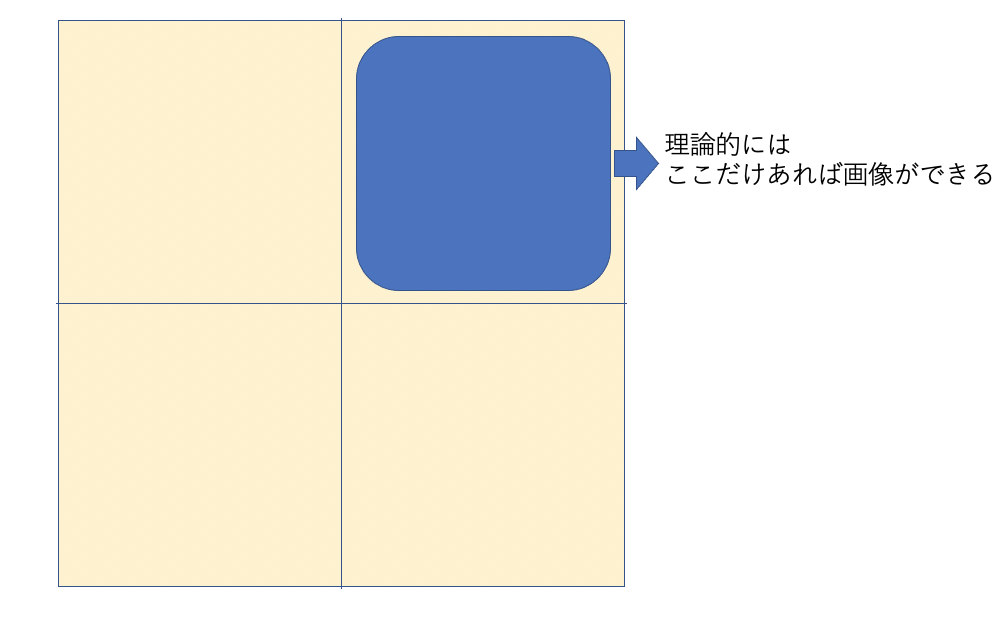
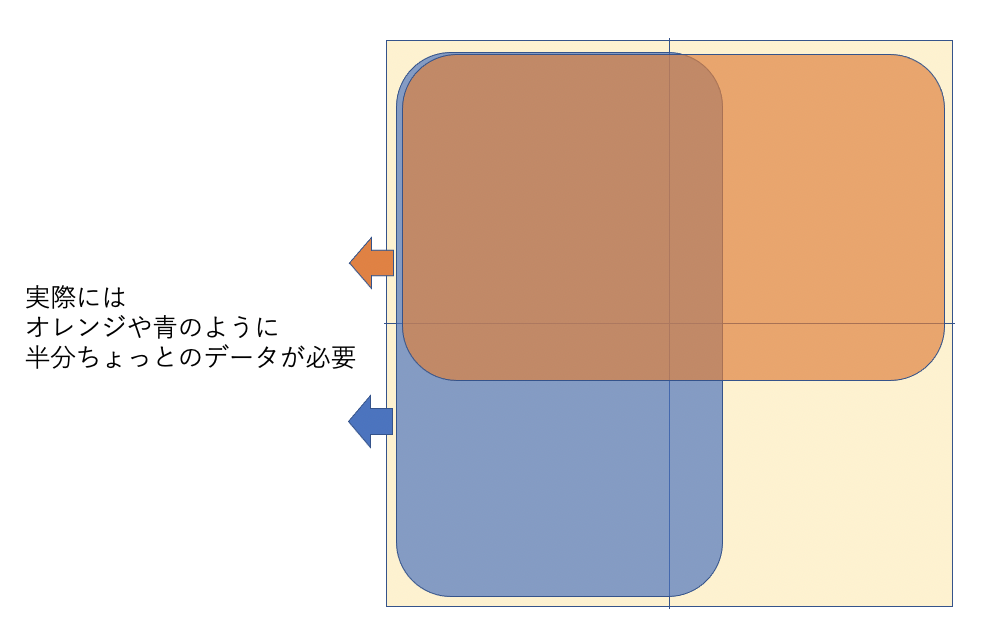
またk空間には場所によって画像に影響する要素が違います。そもそも実画像の一番右上のピクセルとk空間の一番右上の部分は個別に関与しているわけではなく、実画像のある一点はk空間の全てが関与していて、k空間のある一点は実画像の信号が全て関与しています。こんがらがりそうですが、k空間も実画像も互いに one for all、all for one のような関係にあるイメージです。
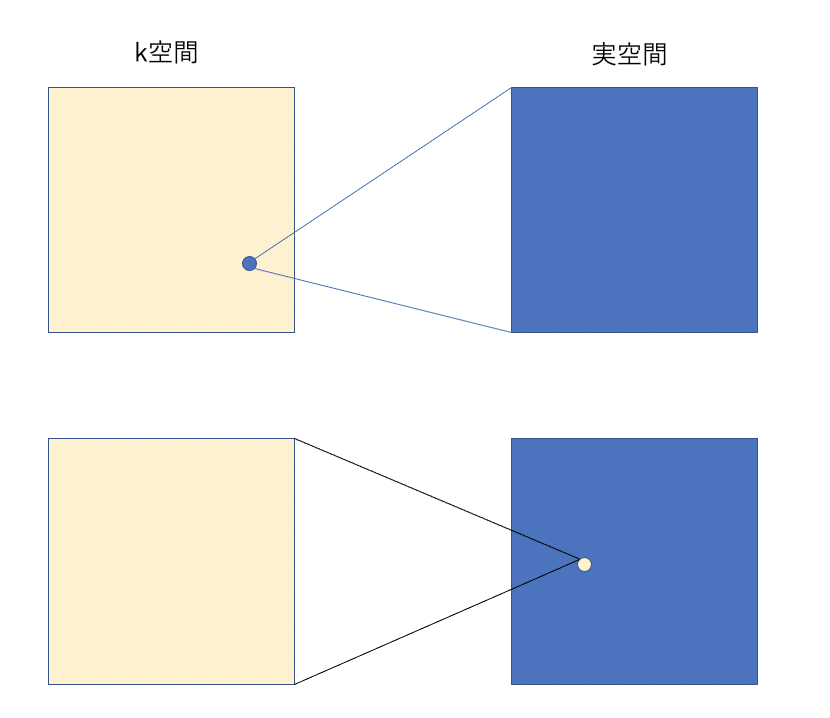
話を戻して、k空間の場所による要素ですが、中心部は主にコントラストや大まかな画像の形状、周辺部が画像の先鋭に関わっています。
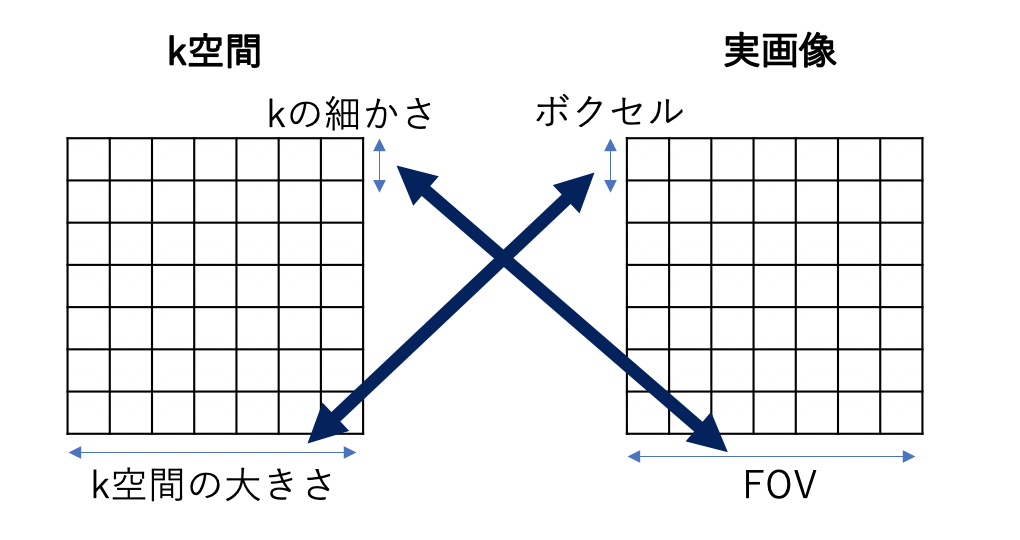
k空間の大きさ細かさと、FOVボクセルサイズの関係ですが、
k空間が細かければFOVは大きくなり、
ボクセルサイズが細かければk空間は大きくなります。
要するにk空間の大きさや細かさは実際の画像のFOVとボクセルサイズに反比例しているということです。
問題について
縦が位相エンコーディング方向(Phase)、横が周波数エンコーディング方向(frequency)となっています。
(1)は基本的な充填方法
(2)はパラレルイメージング
位相エンコードを間引いて信号を取得します。その分早い撮影が可能です。
(3)EPI
SNRは低いものの最速の撮影方法です。
(4)部分エコー法
周波数エンコードを半分取得します。TEを短縮することが可能。
しかしSNRは1/√2=約70%となります。
位相エンコードを半分取得する場合はハーフフーリエ法と呼ばれ撮像時間を約半分にすることが可能ですが約70%となります。
まとめ
k空間についてでしたが、この問題は過去に何度か出題されており抑えておきたい問題だと思います。
参考書籍・文献
MRI完全解説第2版 P150
など
解答に関して、今まで培った知識や書籍・文献を参考に導出したもので、私の認識不足により間違っている可能性もございます。ご理解いただいた上でご参考ください。
MRI認定試験の合格を目指している方のお手伝いができればと思っています。











コメント